无解的游戏

算法基础学习

wxvirus2021年10月12日
大约 7 分钟

简单判断算法的时间复杂度

  • 确定问题规模 n

  • 循环减半过程 logn

  • k 层关于 n 的循环 nk(这边是 n 的 k 次方，可能渲染上有问题)

  • 复杂情况：根据算法的执行过程判断

  • 用常数 1 取代运行时间中的所有加法常数

  • 在修改后的运行次数函数中，只保留最高阶项

  • 如果最高阶项存在且不是 1 ，则去除与这个项相乘的常数

  • 得到的最后结果就是大O阶

常数阶

int sum = 0, n = 100;
printf("hello world\n");
printf("hello world\n");
printf("hello world\n");
printf("hello world\n");
printf("hello world\n");
printf("hello world\n");
printf("hello world\n");
sum = (1+n)*n/2;

上述代码的时间复杂度为：O(1)，不能认为有多少条语句就有多少。

线性阶

int i, n = 100, sum = 0;
for (i = 0; i < n; i++)
{
    sum = sum + i;
}

上述代码，它的循环的时间复杂度为O(n)，因为循环体中的代码需要执行n次

平方阶

int i, j, n = 100;
for (i = 0; i < n; i++)
{
    for (j = 0; j < n; j++) {
        printf("hello world\n");
    }
}

上述代码 2 次循环执行了n²即这段代码的时间复杂度为O(n²)

修改一下：

int i, j, n = 100;
for (i = 0; i < n; i++)
{
    for (j = i; j < n; j++) {
        printf("hello world\n");
    }
}

当i = 0，内循环执行了n次，当i = 1时，内循环则执行n-1次，当i = n - 1时，内循环执行了 1 次，所以总的执行次数应该是：

n+(n−1)+(n−2)+...+1=n(n+1)/2n + (n - 1) + (n - 2) + ... + 1 = n(n + 1) / 2

即高斯先生的等差数列算法，使用推导攻略，第一条忽略，因为没有常数；第二条只保留最高项，所以n/2这项去掉；第三条，去除与最高项相乘的常数，最终得到O(n²)

对数阶

int i = 1, n = 100;
while (i < n)
{
    i = i * 2;
}

每次i*2之后，就会距离n更近一点，假设有x个 2 相乘后大于或等于n则会退出循环

于是由2^x = n得到x = log(2)n，所以这个循环的时间复杂度为O(logn)

举例

n++;
function(n);
for (i = 0; i < n; i++)
{
    function(i);
}

for (i = 0; j < n ; i++)
{
    for (j = i; j < n; j++)
    {
        printf("%d", j);
    }
}

1 + n + n^2 + n^2 即：O(n²)

常见的时间复杂度

例子时间复杂度术语
5201314O(1)常数阶
3n+4O(n)线性阶
3n^2+4n+5O(n^2)平方阶
3log(2)n + 4O(logn)对数阶
2n + 3nlog(2)n + 14O(nlogn)nlogn 阶
n^3+ 2n^2 + 4n + 6O(n^3)立方阶
2^nO(2^n)指数阶

算法初体验

等差数列的实现

#include <stdio.h>

int main(void) {
    int sum, n = 100;
    sum = (1 + n) * n / 2;
    printf("%d", sum);
    return 0;
}

算法特性

  • 输入

    算法具有 0 个输入或多个输入

  • 输出

    • 算法至少有一个或多个输出

  • 有穷性：

    • 算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。

  • 确定性：

    • 算法的每一个步骤都具有确定的含义，不会出现二义性
    • 算法在一定条件下，只有一个执行路径，相同的输入只能有唯一的输出结果
    • 算法的每个步骤都应该被精确定义而无歧义

  • 可行性：

    • 算法的每一步骤都必须是可行的，不能有含糊其辞，也就是每一步都能够通过执行有限次数完成

算法设计的要求

  1. 正确性
    • 算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能得到问题的正确答案
    • 大体分为四个层次：
      • 算法程序没有语法错误
      • 算法程序对合法的输入能够产生满足要求的输出
      • 算法程序对于非法输入能够产生满足规格的说明
      • 算法程序对于故意刁难的测试输入都有满足要求的输出结果
  2. 可读性
    • 算法的设计另一个目的是为了便于阅读、理解和交流
  3. 健壮性
    • 当输入数据不合法时，算法也能做出相关处理，而不是产生异常、崩溃或莫名其妙的结果
  4. 时间效率高和存储量低

空间复杂度

用来评估算法内存占用大小的式子

空间复杂度的表示方式和时间复杂度完全一样

  • 算法使用了几个变量：O(1)
  • 算法使用了长度为 n 的一维列表：O(n)
  • 算法使用了 m 行 n 列的二维列表：O(mn)

提示

现在一般来说时间复杂度比较重要

所以大部分算法都有一个说法：“空间换时间”，比如：分布式的一个运算。

第一种算法执行了 1+(n+1)+n = 2n + 2 次

int i, sum = 0, n = 100; // 执行了1次

for (i = 1; i <= n; i++) // 执行了n + 1 次
{
    sum = sum + i; // 执行了n次
}

第二种算法执行了 1+1=2 次

int sum = 0, n = 100; // 执行了1次
sum = (1 + n) * n / 2; // 执行了1次

函数的渐进式增长

判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项(最高项)的阶数

递归

两个特点：

  • 调用自身
  • 结束条件

四个示例

def func1(x):
    print(x)
    func1(x - 1)

第一个没有结束条件！

def func2(x):
    if x > 0：
    	print(x)
        func2(x + 1)

看似加了结束条件，但是递归条件是+1，不会有小于 0 的时候

def func3(x):
    if x > 0:
        print(x)
        func3(x - 1)

这是一个合法的递归。

案例
x = 3 # 传入

>>>输出结果
3
2
1


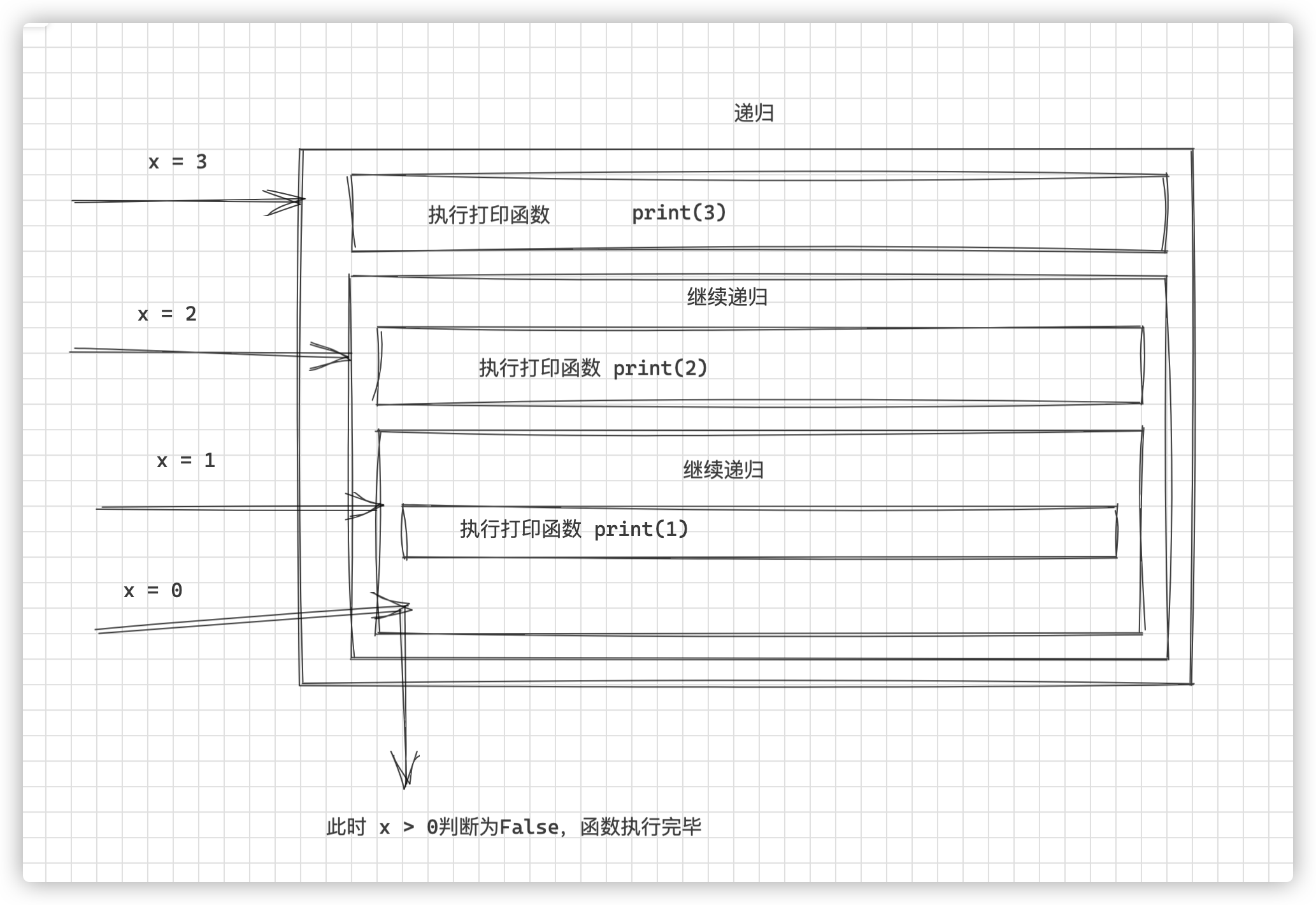
def func4(x):
    if x > 0:
        func4(x - 1)
        print(x)

此函数是先递归后打印，函数执行过程还是从上往下的。

案例
x = 3 # 传入x = 3

>>>输出
1
2
3

汉诺塔问题

由来

提示

大梵天创造世界的时候做了 3 根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。

他命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。

在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

64 根柱子移动完毕之日，就是 世界毁灭之时。

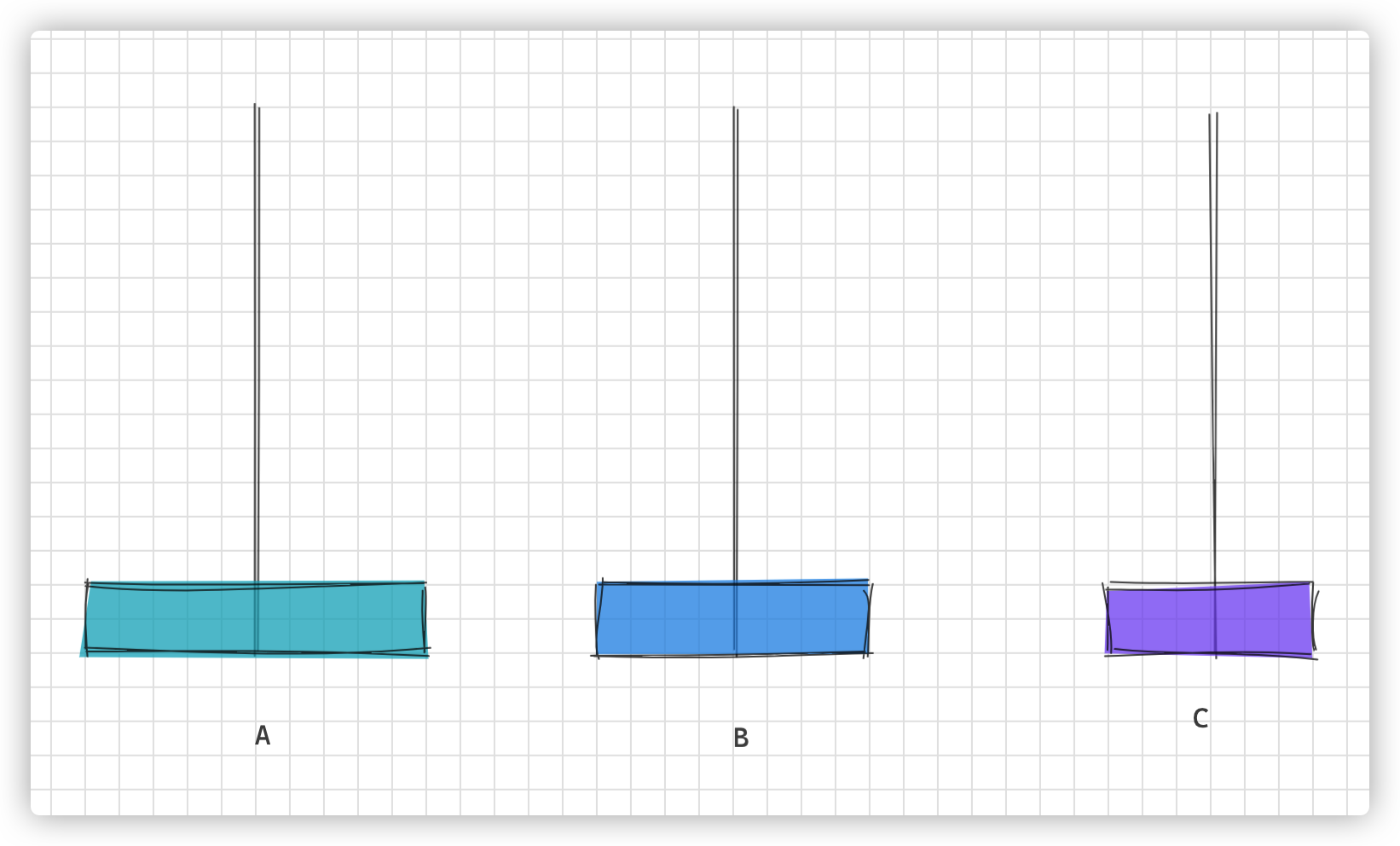
这里把圆盘的个数记作：n

三个柱子分别代表：A,B,C

n = 2 时

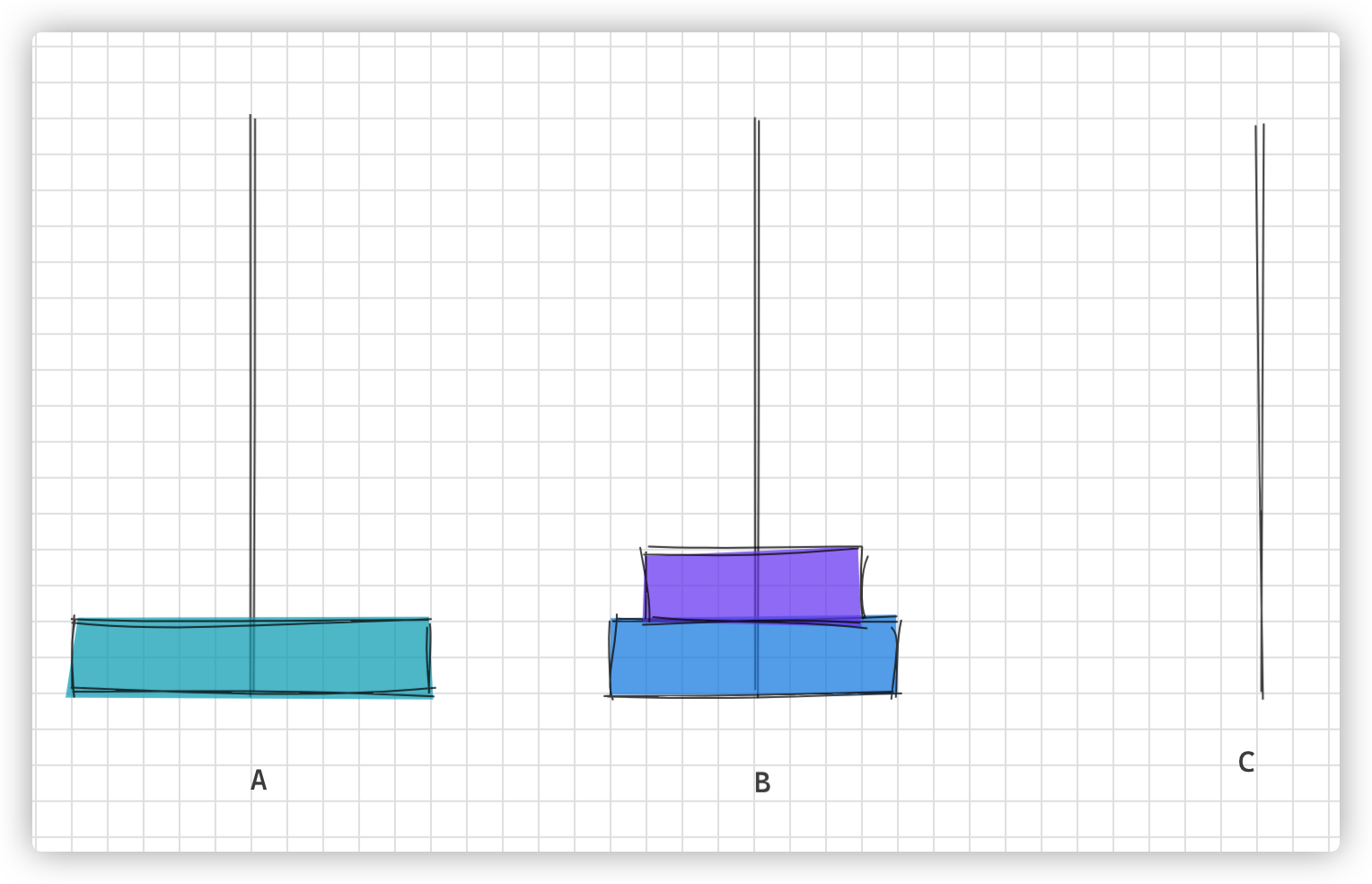
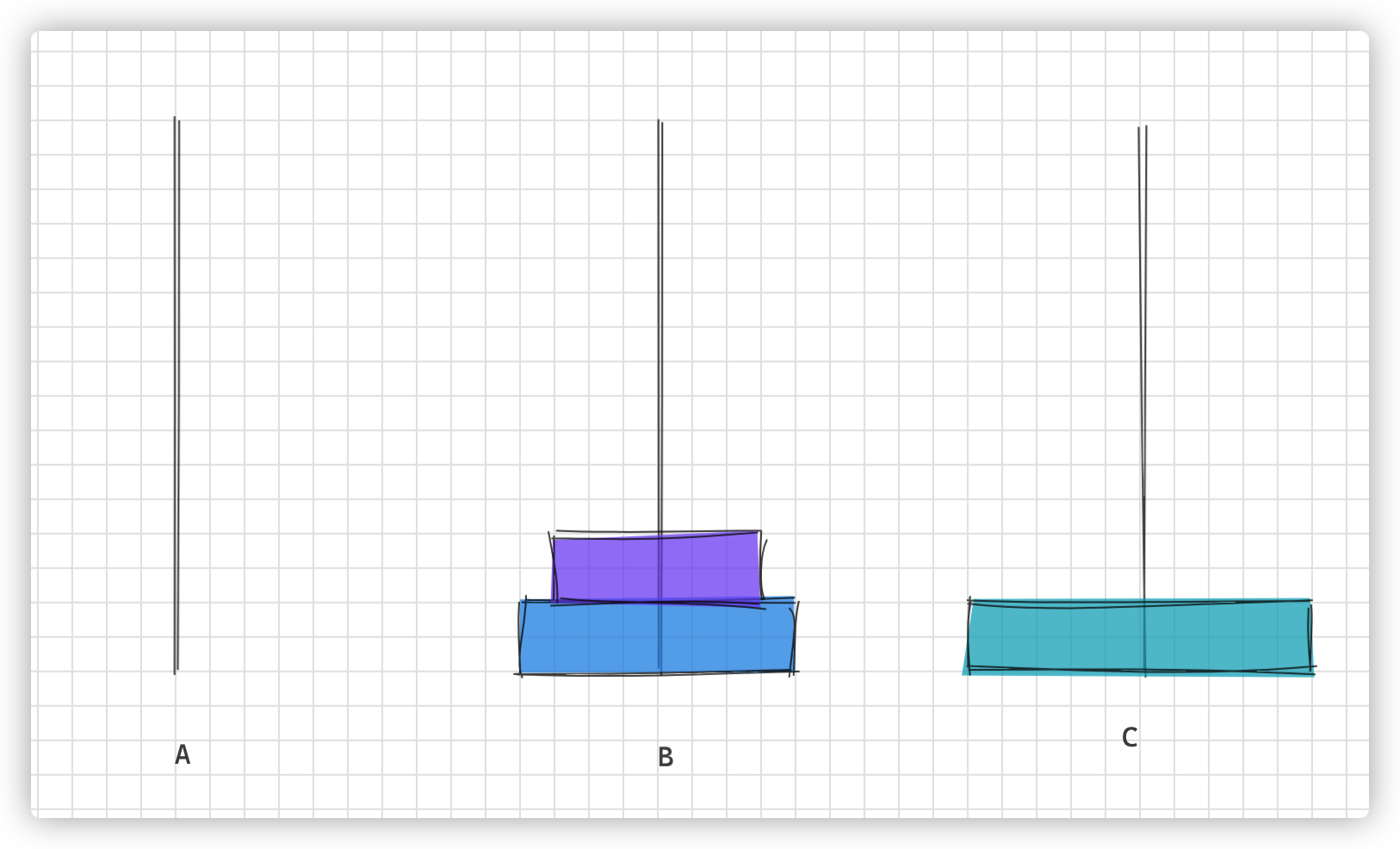
  • 把小圆盘从 A 移动到 B
  • 把大圆盘从 A 移动到 C
  • 把小圆盘从 B 移动到 C

n 个盘子时：

  1. 把 n-1 个盘子从 A 经过 C 移动到 B
  2. 把第 n 个盘子从 A 移动到 C
  3. 把 n-1 个盘子从 B 经过 A 移动到 C

代码：

# -*- coding: utf8 -*-
# @Time    : 2021/10/16 21:52
# @Author  : wxvirus
# @File    : hanoi.py
# @Software: PyCharm
# 汉诺塔算法

def hanoi(n, a, b, c):
    """
    汉诺塔算法
    递归终止条件 n = 0 没有盘子了
    默认参数是从a经过b到c
    :param n: 盘子个数
    :param a: 第一个柱子
    :param b: 第二个柱子
    :param c: 第三个柱子
    :return:
    """
    if n > 0:
        hanoi(n - 1, a, c, b)
        print("moving from {} to {}".format(a, c))
        hanoi(n - 1, b, a, c)


hanoi(3, 'A', 'B', 'C')

这里是一个数学公式啊，因为vuepress我还不会整如何显示数学公式的，可能下面的会多出来几个美元符。这里再写一个没有美元符的：

h(x) = 2h(x - 1) + 1

汉诺塔移动次数的递推式：

h(x)=2h(x−1)+1h(x) = 2h(x - 1) + 1

假设婆罗门每秒钟搬一个盘子，则总共需要 5800 亿年！

# n = 3输出结果

moving from A to C
moving from A to B
moving from C to B
moving from A to C
moving from B to A
moving from B to C
moving from A to C
画图理解步骤

C_B

A_C

B_A

B_C

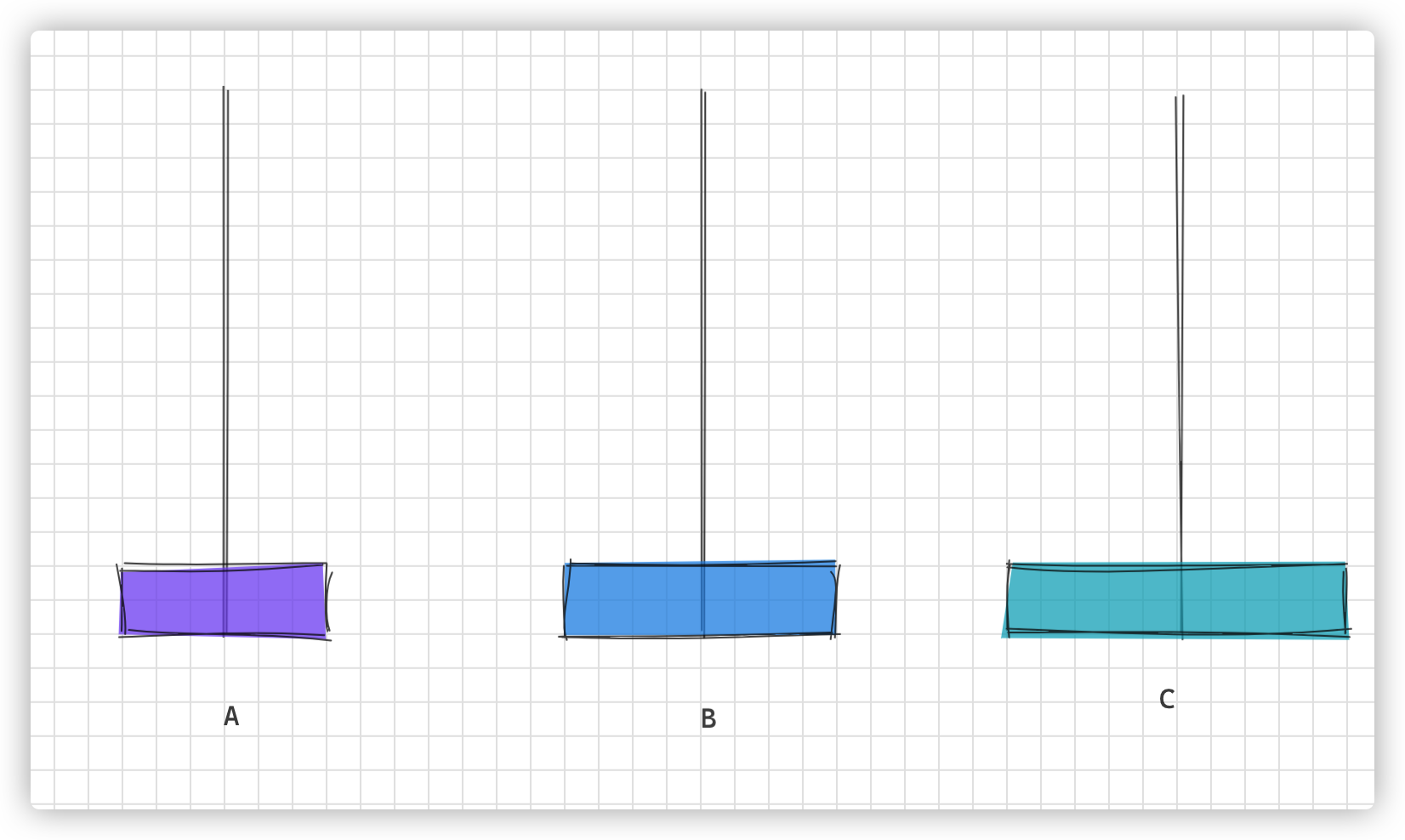
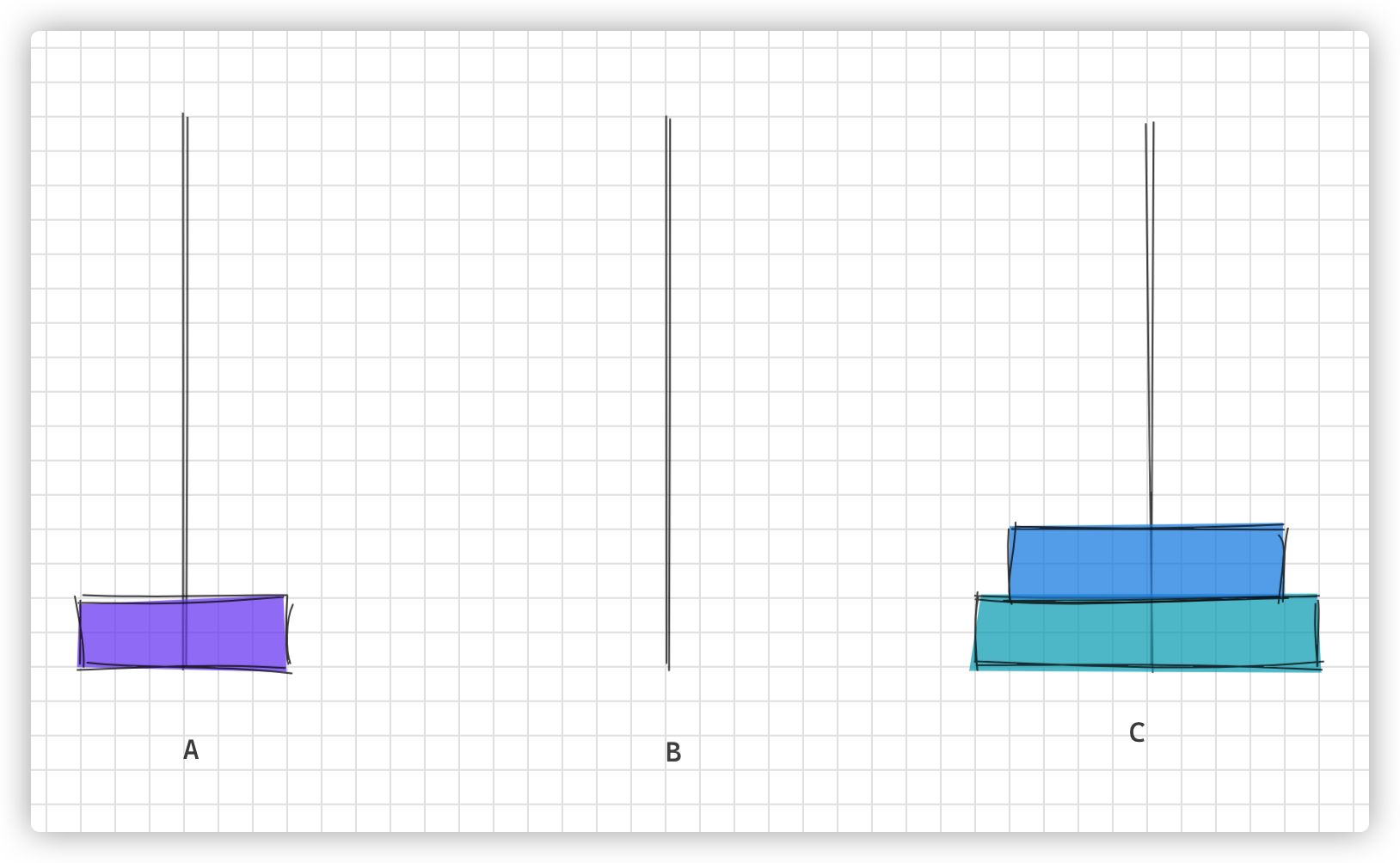
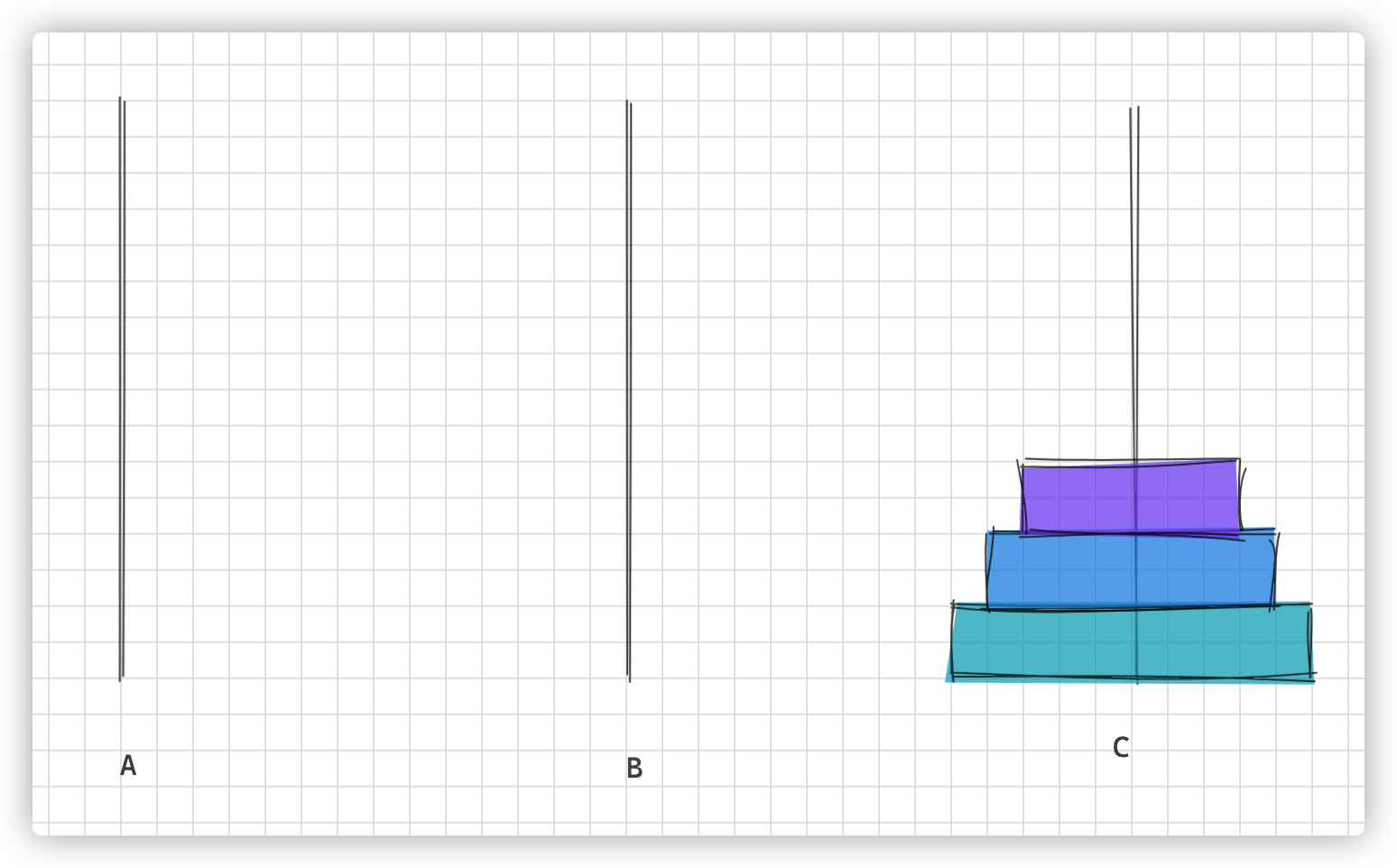
c 语言实现汉诺塔

//
// Created by virus on 2022/5/28.
//
#include <stdio.h>

/**
 * 汉诺塔
 * @param n the count of plates
 * @param src the source of the plates to move from
 * @param dest the destination of the plates to move to
 * @param tmp the temporary place to use
 */
void Move(int n, char src, char dest, char tmp) {
    if (n == 0) return;
    else if (n == 1) printf("%c --> %c\n", src, dest);
    else {
        Move(n - 1, src, tmp, dest);
        Move(1, src, dest, tmp);
        Move(n - 1, tmp, dest, src);
    }
}

int main(void) {
    Move(3, 'A', 'C', 'B');
    return 0;
}


A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C
Loading...
无解的游戏
Copyright © 2024 wxvirus